PLEXOS Hydro Stochastic Optimization

Advanced modeling for inflow uncertainty

Table of Contents

Introduction

Power systems that have both hydro-electric and thermal generation require a systematic and coordinated approach to determine an optimal storage management. The goal of a hydro-thermal planning tool is to minimize the expected thermal costs across the simulation period by dispatching hydro during high-value periods as much as possible. These types of problems generally require stochastic analysis to deal with inflow uncertainty, which increases the mathematical size of the problem and hence are often cumbersome to solve. This white paper reviews the stochastic analysis algorithm in PLEXOS as applied to different hydro-dominated power systems.

PLEXOS Hydro also provides the more traditional Stochastic Dual Dynamic Programming (the SDDP algorithm), which is adequately documented in academic literature. 

Stochastic Optimization

When operating under uncertainty, a decision-maker must make optimal choices throughout a decision horizon with incomplete information. The decision horizon includes many defined stages, in which each stage represents a point in time where the user either makes a decision, or the uncertainty partially or totally vanishes. The amount of information available to the decision maker is usually different from stage to stage. According to the number of stages in the optimization problem, we can distinguish between:

  • Two-stage stochastic problems.
  • Multi-stage stochastic problems.

Two-stage Stochastic Problems

Two-stage applies to a decision-making problem in which decisions are made in two stages, and the existing uncertainty is represented by a set of scenarios or samples. It is a two-step process:

  1. Make a set of decisions.
  2. Profit from the outcome or clean up the mess (recourse actions if any). 

The two-stage stochastic optimization doesn’t allow the user to make revisions after revealing the uncertainty, so it has the following limitations: 

  • The plan for the entire horizon is determined before uncertainty is realized.
  • Only a limited number of recourse actions (if available) can be taken afterwards.
  • Limited use (short-term only) for hydro optimization. Stochastic Hydro Multi-stage Optimization 

Multi-stage Stochastic Problems

When information is slowly revealed over time, we need to adopt a multi-stage approach. The decision-making process for a multi-stage stochastic problem is:

  1. Make a decision for today (t) based on what I know today.
  2. Observe the outcome from stochastic process in time t.
  3. Increment t and repeat until the entire study horizon has been simulated and optimized.

This type of phased decision-making approach allows users to revise over time as more information regarding the uncertainties is revealed.

Multi-stage stochastic optimization has the following upsides and downsides:

  • Upside: It is a better characterization of the dynamic planning process and provides more flexibility than the two-stage model.
  • Downside: Simulation size, memory and runtime increase exponentially as we add more stages.

For medium-long term hydro optimization, the most suitable approach is multi-stage stochastic optimization, and that is the type of optimization problem covered in this paper.

Stochastic Tree Reduction for Multi-stage

When using multi-stage stochastic optimization, the user can generate many possible scenarios, as shown in Figure 1. For such a high number of scenarios, it is impossible to numerically obtain a solution for the multi-stage optimization problem. Different techniques have been introduced in the literature to help solve this problem and commonly involve either a scenario tree reduction or a more simplified tree solved with decomposition techniques.

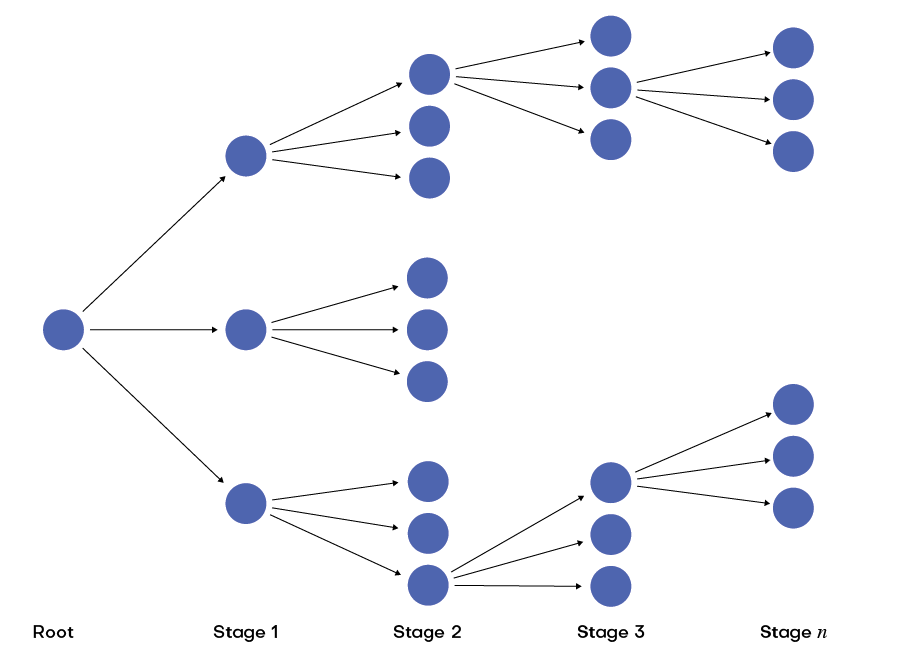
multi-stage dimensiuonality issue
Figure 1: Multi-stage dimensionality issue

In general we will have the number of scenarios are equal to:

Branches_perStage(nStages)

For Example: 21 stages and 3 branches per node
321 = 1.04605 x 1010 scenarios

The 'problem' with multi-stage stochastic optimization is the simulation size/memory/runtime increases exponentially as stages are added, quickly leading to problems that are unfeasible to solve.

PLEXOS offers a scenario-reduction technique called “hanging branches,” which is described in the following section.

Hanging Branches Representation

Assuming we have a multi-stage stochastic problem consisting of four stages and three branches per stage, we can represent the tree as shown in Figure 2.

multi-stage tree

Figure 2: Full multi-stage tree for 4 stages and 3 branches per stage. 3 4= 81 scenarios to explore.

We can reduce this full tree to solve an equivalent multi-stage problem. There are several ways to reduce the stochastic tree: in this paper we reduce the stochastic tree by organizing the branches as “full branches,” “hanging branches” or “death branches,” which are defined as:

  • Full branch: Path to be explored.
  • Hanging branch: Uncertainty associated to the full branch to be explored.
  • Death branch: Path to be discarded to avoid dimensionality issues.

If the user reduces the tree in Figure 2, to in three full branches and two hanging branches per stage, Figure 3 is the resulting tree.

Hanging Tree classification

Figure 3: Full tree classified in full, hanging and death branches

By deleting the death branches from the tree in Figure 3, we have the following reduced tree:

Simplified Hanging branches

INDEPENDENCY

It is important to note that the inflows at the beginning of each stage are known. This means we can solve each full branch independently, as shown in Figure 5.

tree after assuming inflows are known at the beginning of each stage
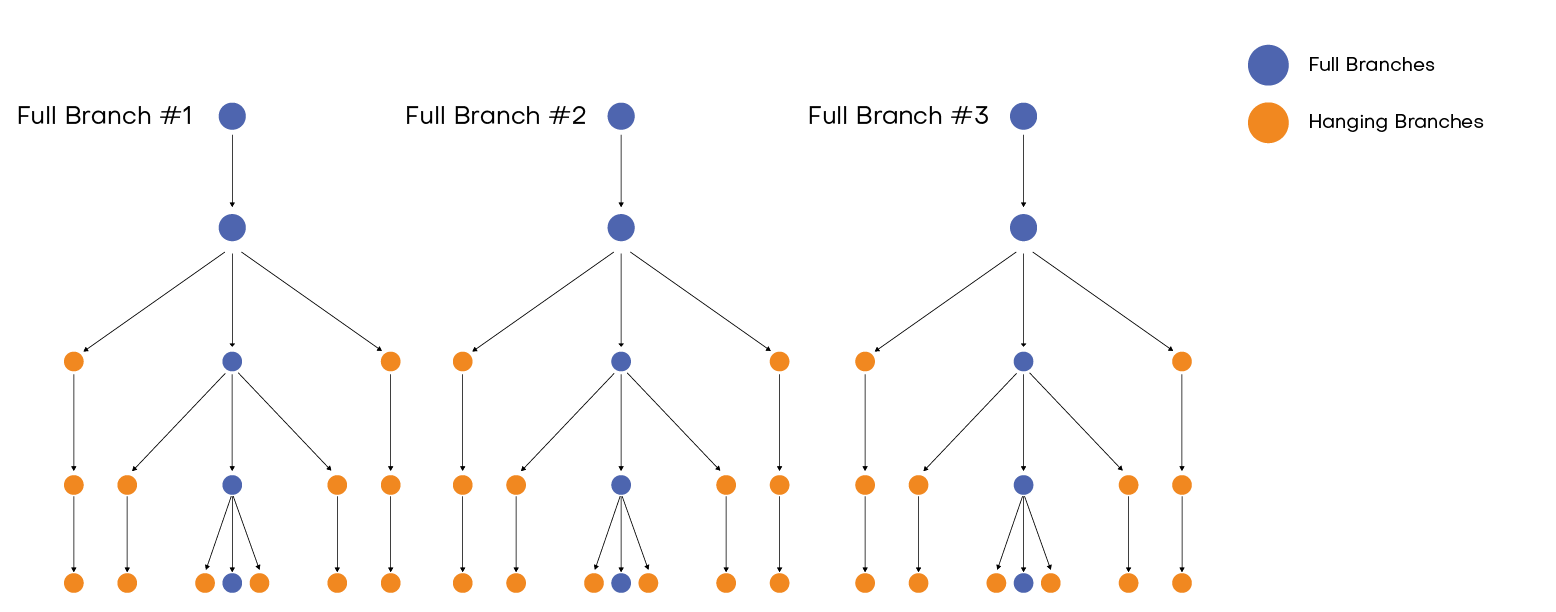
Figure 5: Resulting tree after assuming inflows are known at the beginning of each stage.

Hanging Branches Reduction

By default, the weights for each branch are uniform. In order to avoid dimensionality issues in the number of hanging branches, the user can set the weights used in the objective function for those branches.

We developed a sample reduction algorithm for hanging branches to reduce the number of samples to a predefined smaller number, but the reduced samples are still a good approximation of the original problem. The reduction is based on rules that ensure only the samples that are similar to other samples or have small probabilities are combined. The methodology is illustrated in the following figure:

Hanging Branch Reduction
Figure 6: Hanging branches reduction from 6 to 2 hanging branches per stage.

Rolling Horizon

To solve the resulting tree shown in Figure 5, PLEXOS offers a methodology called “rolling horizon.”

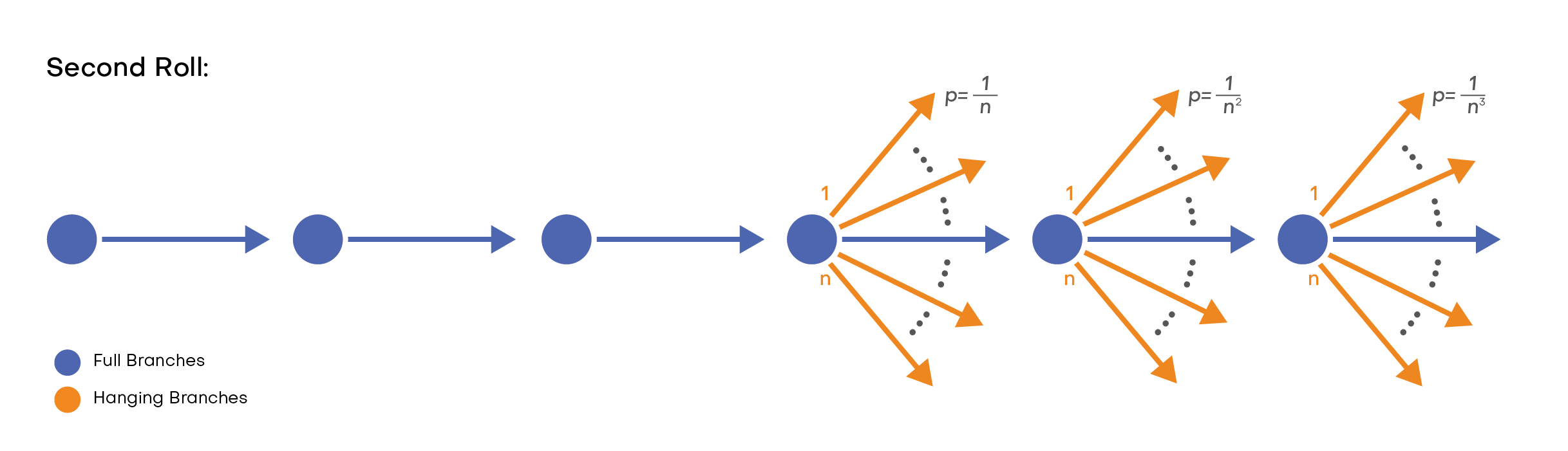
We represent one single, full branch of Figure 5 as follows when solving from a root node:

Rolling Horizon
Figure 7: One single full branch with uncertainty at each stage.

If we formulate 20 or 30 hanging branches per stage, the following weights are generated from root node (see Table 1).

Formulating the multi-stage problem in one single optimization problem produces very small weights for future branches. Commercial solvers can’t guarantee a solution outside the weight range 10^-6 and 10^6.

However, multi-stage stochastic optimization says that at each stage, the decision maker can make a new decision because additional information is revealed. We solve this limitation in the same way a multi-stage stochastic problem is solved in real life: by using a “rolling horizon” approach, which splits the horizon in steps. The only required information we must pass between steps is initial storage and ending volumes.

 

Table 1: Weights from root node
Stage N=20 N=30

1

 0.05 0.0333
2 0.0025 0.0011
3 0.000125 3.7 𝑥 −5
4 6.25𝑥 −6 1.23 𝑥 −6
5 3.13𝑥 −7 4.12 𝑥 −8
6 1.56𝑥 −8 1.37 𝑥 −9
7 7.81𝑥 −10 4.57 𝑥 −11
8 3.91𝑥 −11 1.52 𝑥 −12
9 1.95𝑥−12 5.08 𝑥− 14
10 9.77𝑥− 14 1.69 𝑥− 15

 

The rolling horizon approach is designed to overcome the limitations of extremely small probabilities deep into the future. The method looks ahead to a given point in the future; the end volumes at that point are passed as initial volumes at the start of the next step.

For a horizon divided in multi-step stochastics, the algorithm works as follows:

Step 1:

  1. Starting date is beginning of root node.
  2. Multi-stage tree formulated from start to a user-defined stage in the future where no more branches will be added to avoid weights issue.
First Solve

First roll:

  1. Starting date is beginning of stage 1.
  2. End volumes in first solve are passed as initial volumes in roll 1.
  3. The past branches are not formulated because that part of the problem is already solved.
  4. More hanging branches are formulated when the weights provide information to the optimization solver.
First Roll

Second roll:

  1. Starting date is beginning of stage 2.
  2. End volumes in first roll are passed as initial volumes in roll 2.
  3. The past branches are not formulated because that part of the problem is already solved. 
  4. More hanging branches are formulated when the weights provide information to the optimization solver.
Second Roll

The problem continues rolling until it has fully explored the horizon.

Rolling Horizons

Synthetic Sample Generation

Multi-stage stochastic optimization needs a large number of scenarios, or samples, to represent the equivalent tree. The literature includes different methods for creating these samples, however the simplest method creates future samples based on history.

If we have historical records from 2000 to 2011, and the user wants to create samples from 2019 to 2030, the we need to generate the number of full branches as described in the following table:

Table:2 Historical Information

    Simulated Year
    2019 2020 2021 ... 2028 2029 2030
Full Branches 1 2000 2001 2002 ... 2009 2010 2011
2 2001 2002 2003 ... 2010 2010 2000
3 2002 2003 2004 ... 2011 2000 2001
... ... ... ... ... ... ... ...
... ... ... ... ... ... ... ...
12 2011 2000 2001 ... 2008 2009 2010
... ... ... ... ... ... ... ...

 

This method is powerful and simple, as it preserves the spatial correlation between hydro storages and doesn’t require statistical analysis.

To generate the hanging branches, we can use the historical information as well. For this purpose, the sampling method selects a different year for the same position in time.

A weekly multi-stage problem starting from historical year 2000 could look as follows:

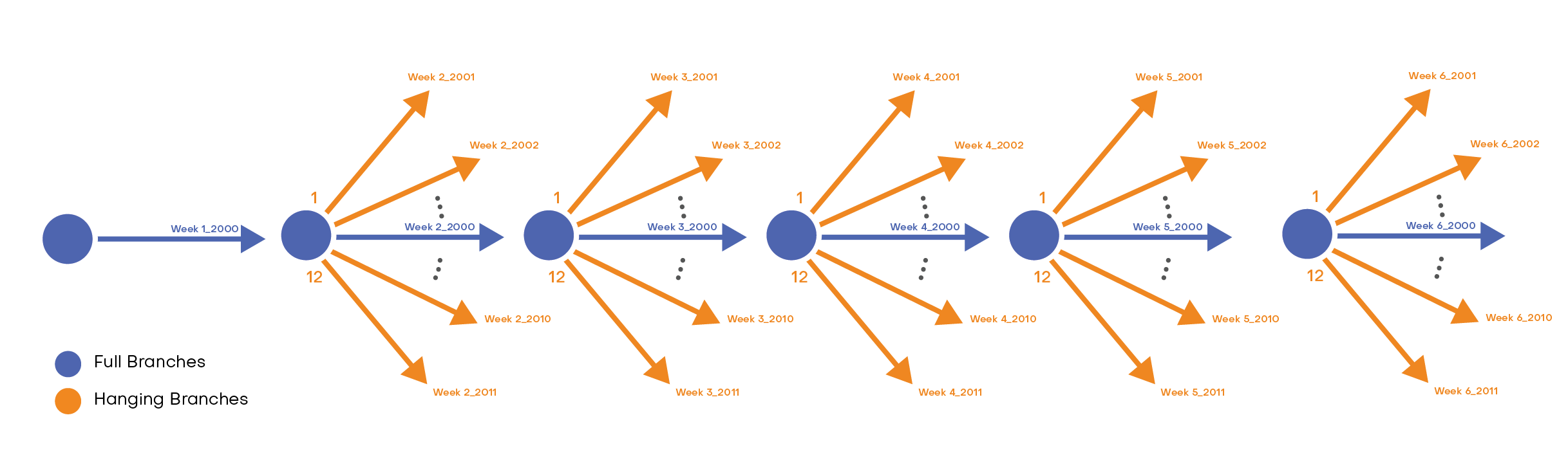
Weekly Solve

The hanging branches for full branch number 1 looks as follows:

Table 3: Hanging branches associated to full branch #1

    Simulated Stage
    Stage 1 Stage 2 Stage 3 ... Stage 10 Stage 11 ...
Hanging Branches 1 Week 2_2001 Week 3_2001 Week 4_2001 ... Week 11_2001 Week 12_2001 ...
2 Week 2_2002 Week 3_2002 Week 4_2002 ... Week 11_2002 Week 12_2002 ...
3 Week 2_2003 Week 3_2003 Week 4_2003 ... Week 11_2003 Week 12_2003 ...
... ... ... ... ... ... ... ...
... ... ... ... ... ... ... ...
12 Week 2_2012 Week 3_2012 Week 4_2012 ... Week 11_2012 Week 12_2012 ...
... ... ... ... ... ... ... ...

 

Conclusion

PLEXOS is a powerful energy system modeling tool that allows users to simulate and optimize energy systems, including power generation, transmission, and distribution. One of the key features of PLEXOS is its ability to model with rolling horizons, making it particularly useful for solving multi-stage stochastic problems in energy systems.

PLEXOS is the globally recognized tool of choice when modeling multi-stage stochastic problems for five primary reasons.

  1. Accuracy: PLEXOS allows users to model complex energy systems accurately, including renewable energy sources and energy storage systems. This accuracy is essential in multi-stage stochastic problems, where the outcomes of decisions made in one period can significantly impact the outcomes in future periods.

  2. Flexibility: PLEXOS is a flexible tool that can handle different types of inputs, such as weather data, demand forecasts, and market prices. This flexibility enables users to adjust their strategies in response to environmental changes, which is essential when uncertainty is high.

  3. Speed: PLEXOS is a fast tool that can handle large amounts of data, making it possible to run simulations quickly and efficiently. This speed is critical in multi-stage stochastic problems, where decision-makers need to evaluate multiple scenarios to determine the best course of action.

  4. Optimization: PLEXOS includes powerful optimization algorithms that allow users to find optimal solutions to complex energy system problems. These algorithms consider multiple objectives, such as minimizing costs and maximizing reliability, and can be used to evaluate different scenarios and strategies.

  5. Visualization: PLEXOS includes a range of visualization tools that allow users to see the results of their simulations clearly and intuitively. This visualization is vital in multi-stage stochastic problems, where decision-makers need to understand the impact of their decisions over time.

Using PLEXOS provides decision-makers with the accuracy, flexibility, speed, optimization, and visualization tools they need to make informed decisions based on the available information while remaining flexible to industry changes.

Take the next step

Uncover the Potential of Precise Modeling and Data-rich Insights.

Request a Sales Consultation